문제
테트리스를 해본 사람이라면 작대기 모양 테트리미노가 나오길 간절히 기다렸던 적이 있을 것이다. 지금 윤성이가 그러하다. 기다리고 기다리던 작대기 모양 테트리미노가 드디어 나온 것이다.
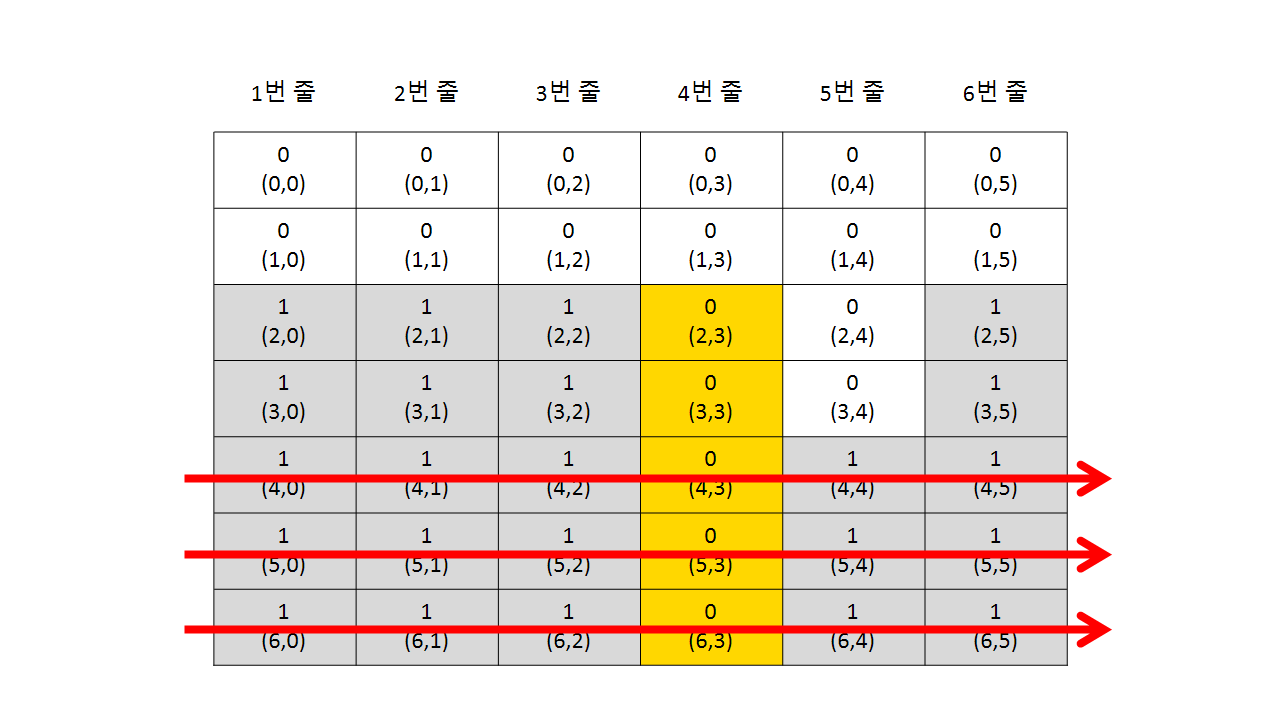
테트리스 맵은 가로로 C칸, 세로로 R칸의 C×R격자형 모양이다. 예를 들어보자. 아래 그림은 가로가 6칸, 세로가 6칸인 테트리스 맵의 상태이다.

(검정색 칸은 이미 메워져있던 칸이고, 회색칸은 이번에 메울 작대기 모양 테트리미노를 의미한다.)
이때 가로가 1칸이고 세로가 4칸인 1×4 직사가형 작대기 모양의 테트리미노(테트리미노는 항상 1×4)를 왼쪽에서 5번째 칸에 둘 경우 총 세줄의 수평선을 메울 수 있다. 테트리스는 한번에 여러 수평선을 메울수록 큰 점수를 얻는 게임이므로, 위 경우에서는 이 방법이 가장 높은 점수를 얻을 수 있는 방법이다.
윤성이를 도와 작대기 모양 테트리미노를 어디에 두었을 때 가장 높은 점수를 얻을 수 있는지 알려주자. (윤성이는 작대기 모양 테트리미노가 나왔을때 게임오버를 당할지언정 가로가 더 길도록 눕혀서 두지 않는다는 나름의 테트리스 철학이 있다.)
그리고 테트리스는 무조건 일자로 떨어진다. (오른쪽에서 왼쪽으로 공간을 비집고 들어가는 등의 스킬은 윤성이에겐 존재하지않는다.)
입력
첫 줄에는 격자 크기를 나타내는 정수 C와 R이 하나의 공백을 사이에 두고 차례대로 주어진다. 두 값의 범위는 5 ≤ C, R ≤ 20이다. 그다음 줄 부터 총 R줄에 걸쳐 맵의 상태를 나타내는 숫자들이 공백을 사이에 두고 주어진다. 0은 아직 채워지지 않은 칸을 나타내며 1은 채워져있는 칸을 나타낸다.
출력
작대기를 왼쪽에서 X번째 자리에 두었을 때 가장 높은 점수를 얻을 수 있고 그 때 완전히 메워지는 수평선의 개수가 Y개라면, Y를 최대로 만드는 X와 그 때의 Y를 하나의 공백을 사이에 두고 출력해야 한다.
만약 어떤 자리에 두어도 수평선을 하나도 메울 수 없거나 게임오버가 일어나는 경우라면 X와 Y를 둘다 0으로 출력한다.(게임오버는 새로 내려온 작대기가 맵상을 벗어난 경우에 일어난다. 새로나온 작대기가 맵의 가장자리에 걸쳐있는 경우는 게임오버가 아니다.)
예제 입력
6 7 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 1 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1
예제 출력
4 3
아이디어
문제를 풀 때 아이디어가 생각이 안 나면 우선 그림을 그려본다.
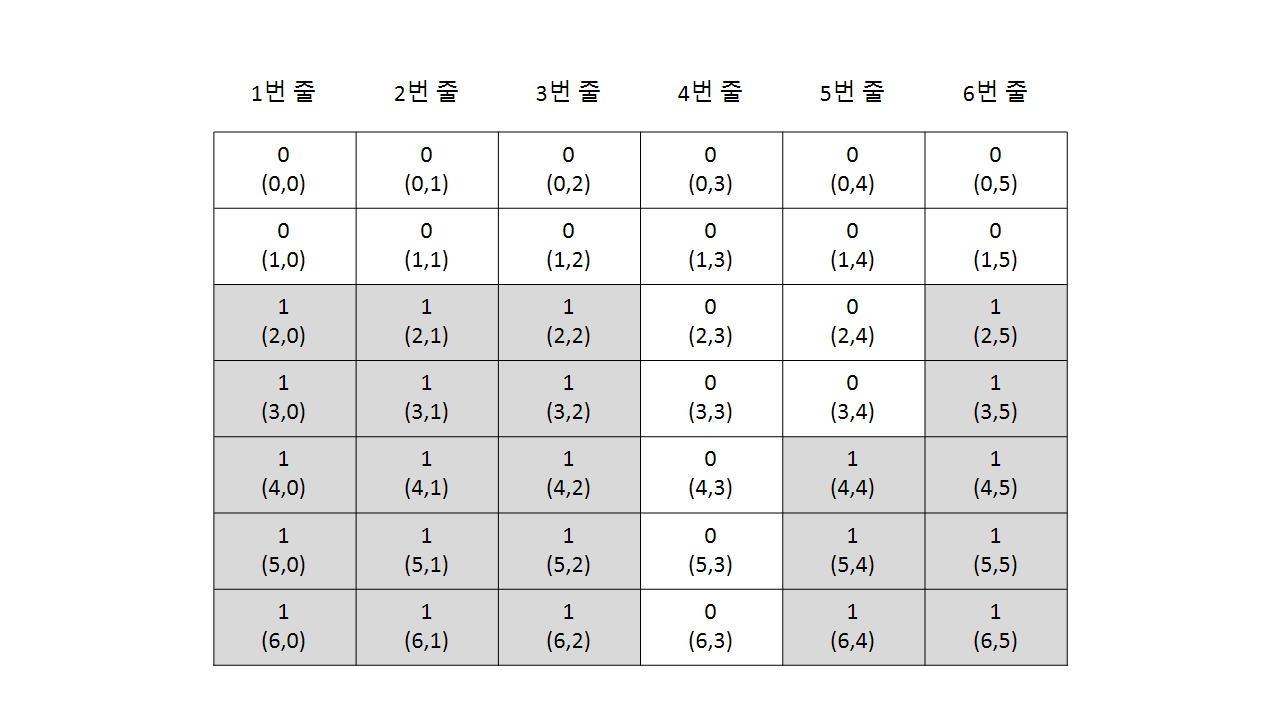
위와 같이 예제로 그림을 그린 뒤 생각해 봤다.
일단 사람이 풀 경우를 생각해 보면 어떻게 풀까?
- 문제 조건에 따라 테트리미노는 항상 1×4이므로 이 경우만 생각하면 된다.
- 그림에서 볼 경우 1번 줄(불가), 2번 줄(불가)…. , 4번 줄(가능), 5번 줄(가능), 6번 줄(불가)
가능 한 경우만 테트리미노를 넣어본다.
![표사진]()
- 위 사진처럼 4번 줄에 테트리미노를 넣었다고 가정하자.
결과는 4번 줄에 넣었고, 수평선으로 3점을 얻는다.(결과 4,3)
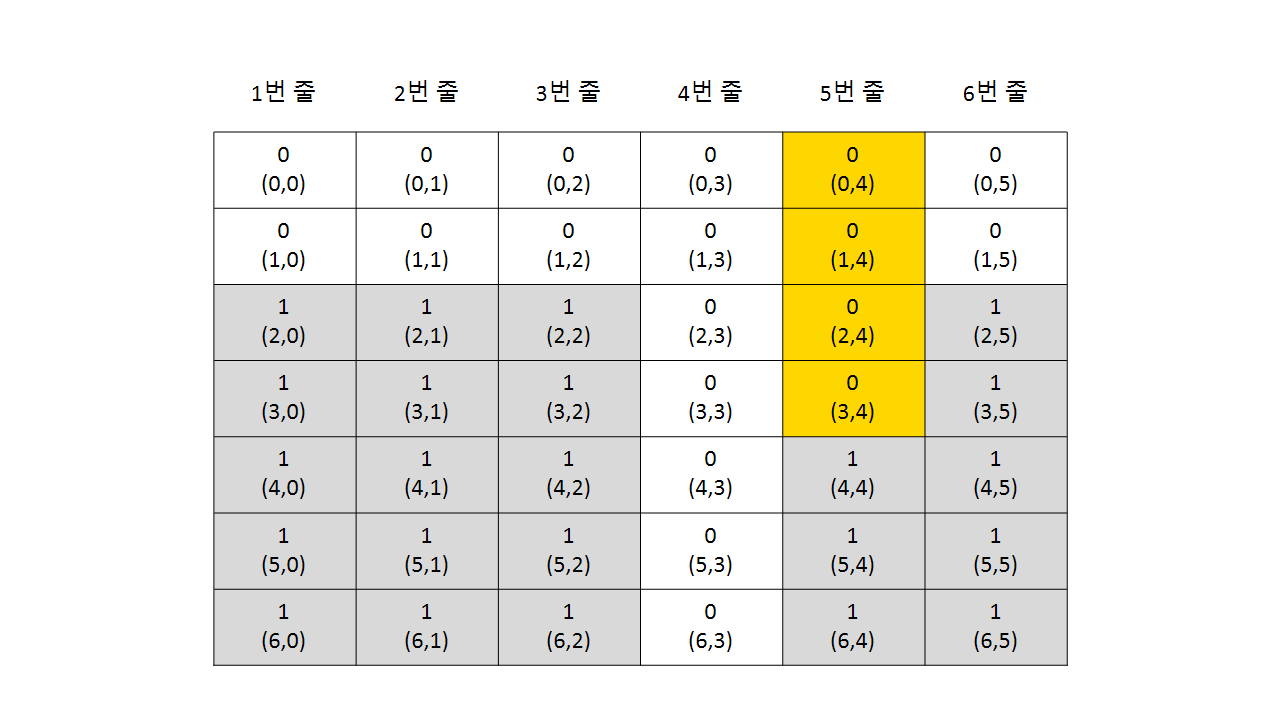
![표사진]()
- 다음 5번 줄에 넣을 수 있는데 5번 줄에 넣어도 수평선이 될 경우는 없다.(결과 0,0)
위와 같이 생각한 뒤 코드로 작성하면 된다. 코드를 간단히 설명하겠다.
- 일단 크게 for 반복문 2개를 사용한다. - n x m의 리스트이니깐.
- 완전탐색으로 n번 줄을 하나씩 살펴본다. - 규칙이 없으니깐 다 살펴봐야 된다.
- 조건에 맞으면(1x4 테트리미노를 넣을 수 있는 경우) 테크리미노를 넣고 수평선과 줄을 기록한다.
- 수평선의 개수가 최대이면 수평선과 줄을 새로 기록한다.
- 다 확인했으면 결과를 출력한다.
- 결과 중 수평선을 기록할 수 없는 경우에는 0,0 수평선을 기록한 경우 수평선, 줄을 출력한다.
코드
풀이보기(클릭)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
n, m = map(int, input().split())
arr = [list(map(int, input().split())) for _ in range(m)]
max = 0
maxRow = -1
for i in range(n): # 가로 0 ~ 5
count = 0
for j in range(m):# 세로 0 ~ 6
if arr[j][i] == 0: # 1 X 4 블록이 내려갈 수 있는 범위
count += 1
else:# 1 X 4 블록이 내려갈 수 없음
break
if count >= 4: # 블록이 내려갈 수 있는 경우
for j in range(count-1,count-5,-1):
arr[j][i] = 1
tmpMax = 0
for j in range(m):
if sum(arr[j]) == n:
tmpMax += 1
if tmpMax > max:
max = tmpMax
maxRow = i
if count >= 4: # arr 리스트 초기화
for j in range(count-1,count-5,-1):
arr[j][i] = 0
if max == 0:
print(0,0)
else:
print(maxRow+1, max)
문제 출처
ALGORITHM JOBS